If you prefer, you can listen to this blog (AI generated text to speech):

What is interleaving and how is it different from spaced practice?
Interleaving is sequencing tasks so that learning material is interspersed with slightly (but not completely) different content or activities. While similar to spaced practice, interleaving involves sequencing tasks or learning content that share some likeness whereas a spaced practice approach uses intervals that are filled with unrelated activities.

How and why does it work?
By repeatedly reintroducing pupils to similar but slightly different content or activities, interleaving is thought to assist the drawing of comparisons between related but discrete items of learning. When completing a series of related activities, pupils may refine their ability to select the more appropriate method for answering certain types of questions.

How does interleaving relate to schemas?
Interleaving draws on the benefits of making comparisons to develop more complex schemas. Schemas (sometimes referred to as mental models, scripts, or frames) are structures that organise knowledge in the mind. When learning, the mind connects new information with pre-existing knowledge, skills, and concepts thereby developing existing schemas. Teachers often want to develop and refine learners’ prior conceptions as opposed to teaching something entirely new.

What does the evidence say?
When compared to a blocked or sequential approach, there is moderate positive evidence that interleaving can better support Key Stage 2 and Key Stage 3 pupils to select appropriate solutions when solving mathematical problems.

There are, however, some important limitations to the evidence: 11 out of 12 studies were in maths, and within these many focused on interleaving tasks that required learners to select a solution strategy before implementing it. While the approach may be transferable across tasks or subjects, we have no evidence to support this.

Case Study:

How I use interleaving and schemas to help students answer synoptic questions - Sarita Sharma, Head of Physics, Barking Abbey School, London

Subject: Physics
Age: KS4
Area of curriculum: Calculations – application of content

Context: In the exam, students have to answer questions where they link a number of ideas. I use ideas around schemas and interleaving to help them practise making these sorts of links, while thinking about how best to approach a question.

How I use schemas: To help students practise making links between ideas, I choose two seemingly unrelated items, and ask them to make links between one and the other in a few steps. For example, consider the AQA GCSE Physics question below.

To answer this question, students need to make links between two seemingly unrelated ideas: satellite motion and induced current. I encourage students to link them, separately from answering the question itself. This can be done as follows:

The students then use this sequence to write their final answer.

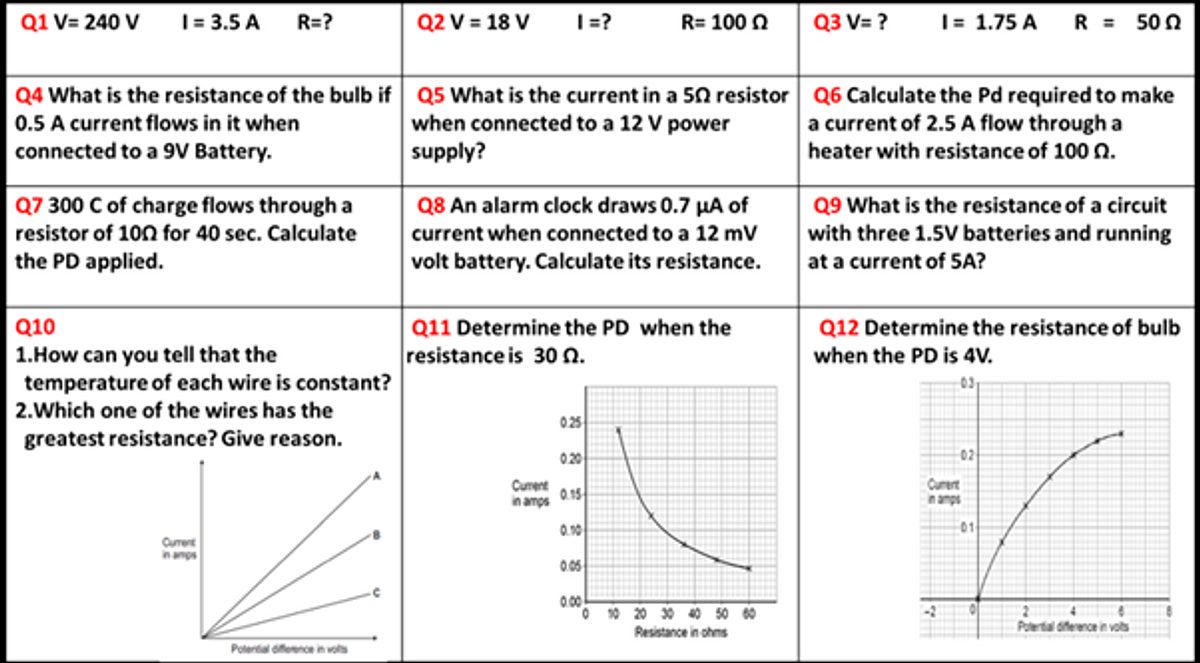
How I use interleaving: To help students think about the approach to a question, rather than following a ​“recipe”, I ask a series of questions that are similar, but demand differing methods to answer.

Example 1: In this set of questions about the relationship between V, I and R (voltage, current and resistance), each has a different focus, and demands a slightly different method each time. Questions are deliberately set out in a way that prevents students from focussing on one variable or skill without considering how and why to approach the question in this way.

This also gives students a chance to apply skills they’ve used in other topics or subjects (for example, unit conversions, gradients, rearranging equations) in a new context. This helps them to build fluency, as they become more used to applying skills without explicit build up to it within the lesson.

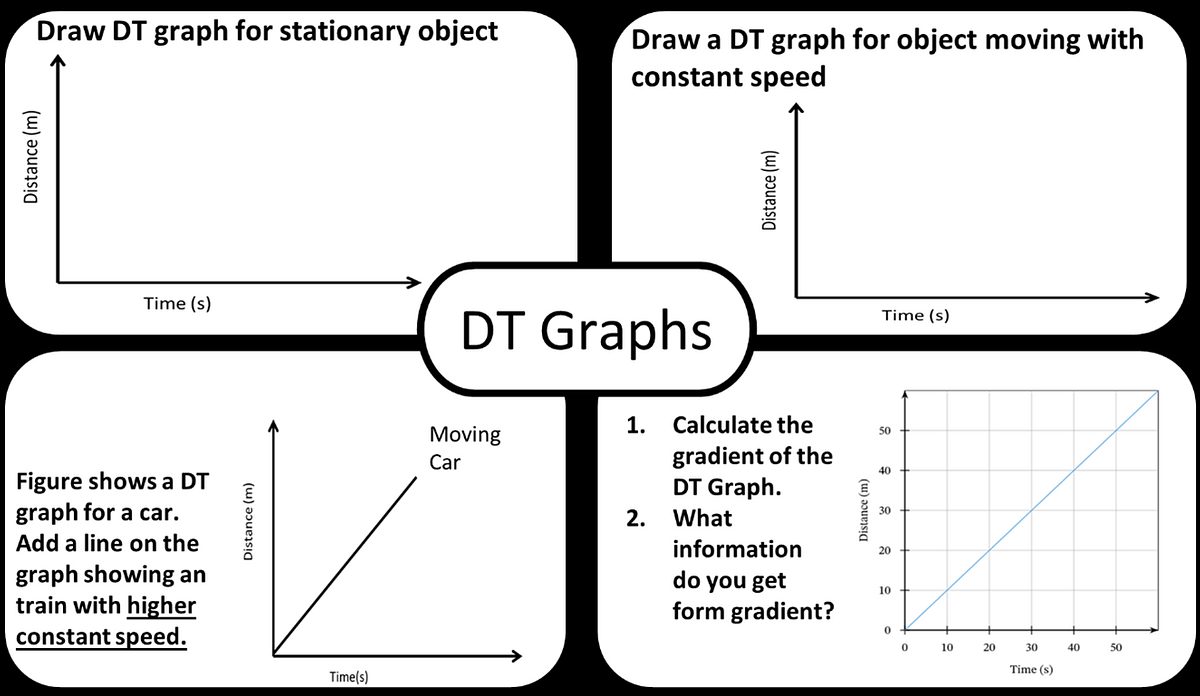
Example 2: I also adapt the Frayer Model in my lessons, which helps support interleaving of skills and concepts. For example, in the two tasks below, maths skills such as interpreting graphs, calculating gradient and areas under curves are interleaved. Students can also see the links between the shapes of DT & VT graphs for similar scenarios but with contrasting objects (stationary vs moving with constant velocity).

Reflections: The strategies used and discussed here are all examples of ​‘Desirable Difficulties’ (eg. Bjork and Bjork, 2011). If used carefully, these strategies really support students to understand how to apply equations to different contexts. However, all of this would be pointless if the students didn’t have background knowledge in the first place. In other words, if I haven’t taught them to rearrange equations, convert units or calculate gradients before doing these exercises, students will not be able to practice these skills and retrieve them effectively when required. Tasks such as the adapted Frayer model can also be used as a spaced retrieval practice task.